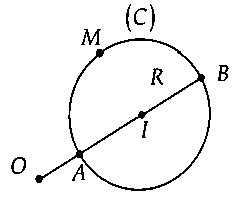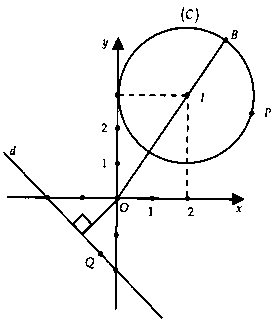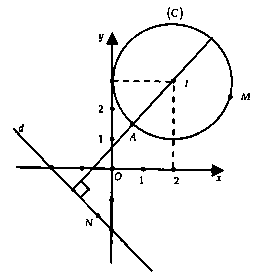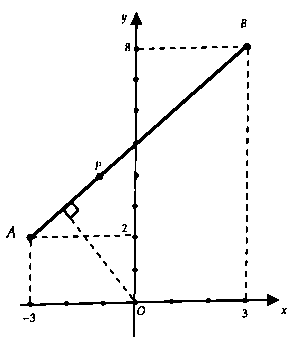Bài viết hướng dẫn phương pháp giải bài toán tìm giá trị lớn nhất và giá trị nhỏ nhất của môđun số phức thỏa mãn điều kiện cho trước (cách gọi khác: GTLN – GTNN môđun số phức, Min – Max môđun số phức) trong chương trình Giải tích 12, đây là dạng toán vận dụng cao (nâng cao, khó) thường gặp trong các đề thi trắc nghiệm Toán 12 và đề thi THPT Quốc gia môn Toán.
Đang xem: Tìm giá trị lớn nhất nhỏ nhất của số phức
I. PHƯƠNG PHÁP GIẢI TOÁN1. Phương pháp chung+ Tìm tập hợp điểm biểu diễn các số phức $z$ thỏa điều kiện cho trước.+ Vẽ tập hợp điểm biểu diễn lên hệ trục, từ đó suy ra kết quả.
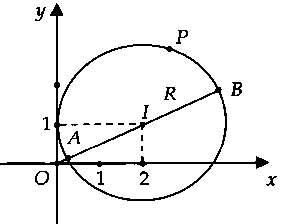
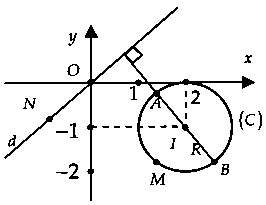
2. Một số kết quả thường dùnga) Bài toán 1: Trong mặt phẳng, cho điểm $O$ và đường tròn $C(I;R)$ cố định, $M$ là điểm di động trên đường tròn đó. Tìm $O{M_{min }}$, $O{M_{max }}.$+ Nếu $O$ nằm ngoài đường tròn thì:$O{M_{min }} = OA = OI – R.$$O{M_{max }} = OB = OI + R.$
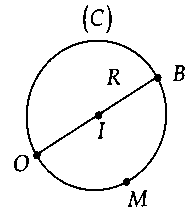
+ Nếu $O$ nằm trên đường tròn thì:$O{M_{min }} = 0.$$O{M_{max }} = OB = 2R.$
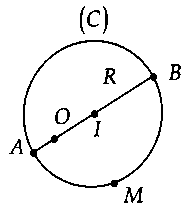
+ Nếu $O$ nằm trong đường tròn thì:$O{M_{min }} = OA = R – OI.$$O{M_{max }} = OB = OI + R.$
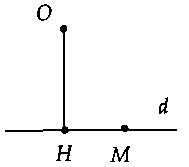
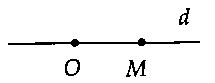
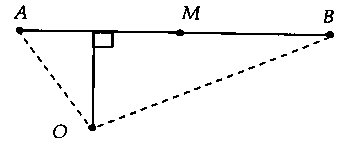
b) Bài toán 2: Trong mặt phẳng, cho điểm $O$ và đường thẳng $d$ cố định, $M$ là điểm di động trên đường thẳng đó. Tìm $O{M_{min }}.$+ Nếu $O$ nằm ngoài đường thẳng $d$ thì: $O{M_{min }} = OH = d(O;d).$
+ Nếu $O$ nằm trên đường tròn thì $O{M_{min }} = 0.$
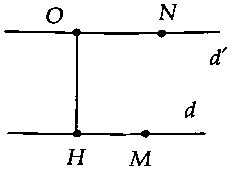
c) Bài toán 3: Trong mặt phẳng, cho hai đường thẳng phân biệt $d$, $d’$ cố định; $M$ là điểm di động trên đường thẳng $d$ và $N$ là điểm di động trên đường thẳng $d’.$ Tìm $M{N_{min }}.$+ Nếu $d//d’$ thì $M{N_{min }} = OH = dleft( {d;d’}
ight).$
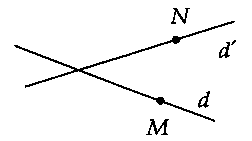
+ Nếu $d$ và $d’$ cắt nhau thì $M{N_{min }} = 0.$
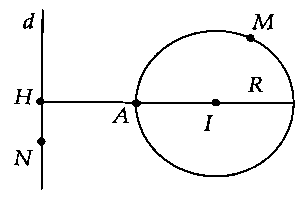
d) Bài toán 4: Trong mặt phẳng, cho hai đường thẳng $d$ và đường tròn $C(I;R)$ cố định và không có điểm chung với nhau; $M$ là điểm di động trên đường thẳng $d$ và $N$ là điểm di động trên đường tròn $C(I;R).$ Tìm $M{N_{min }}.$
$M{N_{min }} = AH = d(I;d) – R.$
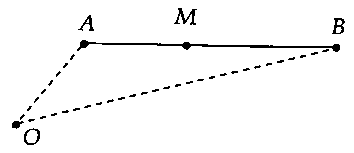
e) Bài toán 5: Trong mặt phẳng, cho ba điểm $O$, $A$, $B$ cố định không thẳng hàng; $M$ là điểm di động trên đoạn thẳng $AB.$ Tìm $O{M_{min }}$, $O{M_{max }}.$+ Nếu $widehat {AOB}$ là góc nhọn thì:$O{M_{min }} = min { OA;OB} .$$O{M_{max }} = max { OA;OB} .$
+ Nếu $widehat {AOB}$ là góc tù thì:$O{M_{min }} = d(O;AB).$$O{M_{max }} = max { OA;OB} .$
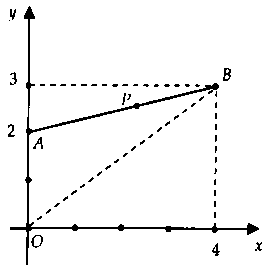
II. BÀI TẬP TRẮC NGHIỆM MINH HỌAVí dụ 1: Cho số phức $z$ thỏa mãn điều kiện $|z – 1 – 2i| = 2.$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z|.$ Giá trị $M + m$ bằng?A. $2sqrt 5 .$B. $sqrt 5 .$C. $sqrt 5 + 2.$D. $sqrt 5 – 2.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.
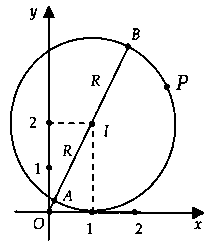
Ta có: $|z – 1 – 2i| = 2$ $ Leftrightarrow {(x – 1)^2} + {(y – 2)^2} = 4.$Suy ra tập hợp điểm biểu diễn các số phức $z$ là đường tròn $(C)$ có tâm $I(1;2)$ và bán kính $R = 2.$Từ hình vẽ, ta có:$M = |z{|_{max }} = OB = OI + R$ và $m = |z{|_{min }} = OA = OI – R.$Vậy $M + m = 2OI$ $ = 2sqrt {{1^2} + {2^2}} = 2sqrt 5 .$Chọn đáp án A.Chú ý: Nếu $(C)$ qua gốc tọa độ $O$ thì $m =0$, $M = 2R.$
Ví dụ 2: Cho số phức $z$ thỏa mãn điều kiện $|z – 2 + i| = 1.$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z|.$ Giá trị $M+3m$ bằng:A. $4sqrt 5 – 4.$B. $4sqrt 5 – 2.$C. $2sqrt 5 + 2.$D. $2sqrt 5 – 2.$
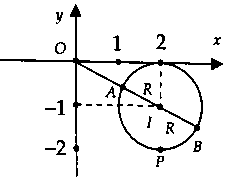
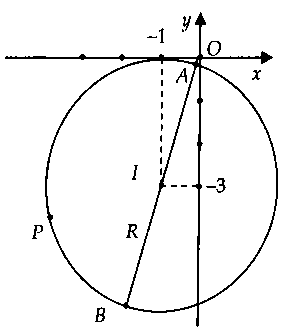
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.Ta có: $|z – 2 + i| = 1$ $ Leftrightarrow {(x – 2)^2} + {(y + 1)^2} = 1.$Suy ra tập hợp điểm biểu diễn các số phức $z$ là đường tròn $(C)$ có tâm $I(2;-1)$ và bán kính $R=1.$
Từ hình vẽ, ta có:$M = |z{|_{max }} = OB = OI + R$ và $m = |z{|_{min }} = OA = OI – R.$Vậy $M + 3m = 4OI – 2R = 4sqrt 5 – 2.$Chọn đáp án B.
Ví dụ 3: Cho số phức $z$ thỏa mãn điều kiện $|z + i| = sqrt 2 |z – 1|.$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z|.$ Giá trị ${M^2} – {m^2}$ bằng?A. ${9.}$B. ${8sqrt 5 .}$C. ${4sqrt 5 .}$D. ${2sqrt 5 .}$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.Ta có: $|z + i| = sqrt 2 |z – 1|.$$ Leftrightarrow sqrt {{x^2} + {{(y + 1)}^2}} $ $ = sqrt 2 sqrt {{{(x – 1)}^2} + {y^2}} .$$ Leftrightarrow {x^2} + {y^2} + 2y + 1$ $ = 2left( {{x^2} – 2x + 1 + {y^2}}
ight).$$ Leftrightarrow {x^2} + {y^2} – 4x – 2y + 1 = 0.$Suy ra tập hợp điểm biểu diễn các số phức $z$ là đường tròn $(C)$ có tâm $I(2;1)$ và bán kính $R = 2.$
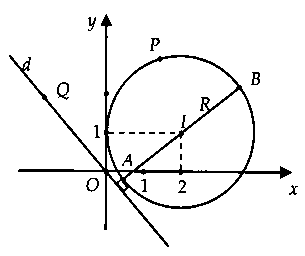
Từ hình vẽ, ta có: $M = |z{|_{max }} = OB = OI + R$ và $m = |z{|_{min }} = OA = OI – R.$Vậy ${M^2} – {m^2}$ $ = {(OI + R)^2} – {(OI – R)^2}$ $ = 4OI.R = 8sqrt 5 .$Chọn đáp án B.
Ví dụ 4: Cho số phức $z$ thỏa mãn điều kiện $|z + i| = 3.$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z – 1 – 2i|.$ Giá trị $M + 2m$ bằng?A. $27.$B. $21.$C. $3sqrt {10} – 3.$D. $3sqrt {10} – 9.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.Ta có: $|z + i| = 3$ $ Leftrightarrow {x^2} + {(y + 1)^2} = 9.$$ Leftrightarrow {<(x – 1) + 1>^2} + {<(y – 2) + 3>^2} = 9.$Ta có số phức $z – 1 – 2i$ có điểm biểu diễn là $P”(x – 1;y – 2).$ Suy ra tập hợp điểm biểu diễn các số phức $z – 1 – 2i$ là đường tròn $(C)$ có tâm $I( – 1; – 3)$ và bán kính $R=3.$
Từ hình vẽ, ta có:$M = |z – 1 – 2i{|_{max }}$ $ = OB = OI + R$ và $m = |z – 1 – 2i{|_{min }}$ $ = OA = OI – R.$Vậy $M + 2m = 3OI – R = 3sqrt {10} – 3.$Chọn đáp án C.
Ví dụ 5: Cho số phức $z$ thỏa mãn điều kiện $|z – 2 – i| = |z + 1|.$ Gọi $m$ là giá trị giá trị nhỏ nhất của $|z|.$ Giá trị $m$ bằng?A. $2.$B. $frac{{sqrt {10} }}{5}.$C. $frac{2}{3}.$D. $frac{1}{5}.$
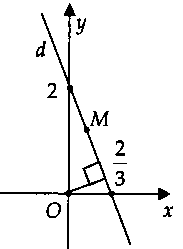
Lời giải:Gọi $M(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.Ta có: $|z – 2 – i| = |z + 1|.$$ Leftrightarrow sqrt {{{(x – 2)}^2} + {{(y – 1)}^2}} $ $ = sqrt {{{(x + 1)}^2} + {y^2}} .$$ Leftrightarrow {x^2} – 4x + 4 + {y^2} – 2y + 1$ $ = {x^2} + 2x + 1 + {y^2}.$$ Leftrightarrow 3x + y – 2 = 0.$Suy ra tập hợp điểm biểu diễn các số phức $z$ là đường thẳng $d:$ $3x + y – 2 = 0.$
Từ hình vẽ, ta có:$m = |z{|_{min }} = d(O;d)$ $ = frac{{|3.0 + 1.0 – 2|}}{{sqrt {{3^2} + {1^2}} }} = frac{{sqrt {10} }}{5}.$Chọn đáp án B.Chú ý: Nếu $d$ qua gốc tọa độ $O$ thì $m =0.$
Ví dụ 6: Trong các số phức thỏa mãn điều kiện $|z – 1 – i| = |z – 2i|.$ Tìm số phức $z$ có môđun nhỏ nhất.A. $z = frac{1}{2} – frac{1}{2}i.$B. $z = frac{1}{2} + frac{3}{2}i.$C. $z = – frac{1}{2} + frac{1}{2}i.$D. $z = frac{3}{2} – frac{1}{2}i.$
Lời giải:Đặt $z = x + yi$ $(x,y in R).$Ta có $|z – 1 – i| = |z – 2i|$ $ Leftrightarrow {(x – 1)^2} + {(y – 1)^2}$ $ = {x^2} + {(y – 2)^2}$ $ Leftrightarrow y = x + 1.$$|z| = sqrt {{x^2} + {y^2}} $ $ = sqrt {2{x^2} + 2x + 1} $ $ = sqrt {2{{left( {x + frac{1}{2}}
ight)}^2} + frac{1}{2}} ge frac{{sqrt 2 }}{2}.$Do đó $|z|$ nhỏ nhất khi và chỉ khi $x = – frac{1}{2}$, $y = frac{1}{2}$ $ Rightarrow z = – frac{1}{2} + frac{1}{2}i.$Chọn đáp án C.
Ví dụ 7: Cho số phức ${z_1}$ thỏa mãn điều kiện $left| {{z_1} – 1 – i}
ight| = left| {{z_1} – 2}
ight|$, số phức ${z_2}$ thỏa mãn điều kiện $left| {{z_2} – 1}
ight| = left| {{z_2} – i}
ight|.$ Gọi $m$ là giá trị giá trị nhỏ nhất của $left| {{z_2} – {z_1}}
ight|.$ Giá trị $m$ bằng?A. $2.$B. $frac{1}{2}.$C. $frac{{sqrt 2 }}{2}.$D. $frac{{sqrt 3 }}{3}.$
Lời giải:Gọi ${P_1}left( {{x_1};{y_1}}
ight)$ là điểm biểu diễn của số phức ${z_1} = {x_1} + {y_1}i$ $left( {{x_1};{y_1} in R}
ight)$ trên mặt phẳng tọa độ.Ta có: $left| {{z_1} – 1 – i}
ight| = left| {{z_1} – 2}
ight|$ $ Leftrightarrow sqrt {{{left( {{x_1} – 1}
ight)}^2} + {{left( {{y_1} – 1}
ight)}^2}} $ $ = sqrt {{{left( {{x_1} – 2}
ight)}^2} + y_1^2} .$$ Leftrightarrow x_1^2 – 2{x_1} + 1 + y_1^2 – 2{y_1} + 1$ $ = x_1^2 – 4{x_1} + 4 + y_1^2.$$ Leftrightarrow {x_1} – {y_1} – 1 = 0.$Suy ra tập hợp điểm biểu diễn các số phức ${z_1}$ là đường thẳng ${d_1}:x – y – 1 = 0.$Gọi ${P_2}left( {{x_2};{y_2}}
ight)$ là điểm biểu diễn của số phức ${z_2} = {x_2} + {y_2}i$ $left( {{x_2};{y_2} in R}
ight)$ trên mặt phẳng tọa độ.Ta có: $left| {{z_2} – 1}
ight| = left| {{z_2} – i}
ight|.$$ Leftrightarrow sqrt {{{left( {{x_2} – 1}
ight)}^2} + y_2^2} = sqrt {x_2^2 + {{left( {{y_2} – 1}
ight)}^2}} $ $ Leftrightarrow {x_2} – {y_2} = 0.$Suy ra tập hợp điểm biểu diễn các số phức ${z_2}$ là đường thẳng: ${d_2}:x – y = 0.$Ta có: $left| {{z_2} – {z_1}}
ight|$ $ = sqrt {{{left( {{x_2} – {x_1}}
ight)}^2} + {{left( {{y_2} – {y_1}}
ight)}^2}} $ $ = {P_1}{P_2}$ $ Rightarrow {left| {{z_2} – {z_1}}
ight|_{min }} = dleft( {{d_1};{d_2}}
ight).$Vì $O in {d_2}$ $ Rightarrow {left| {{z_2} – {z_1}}
ight|_{min }} = dleft( {{d_1};{d_2}}
ight)$ $ = dleft( {O;{d_1}}
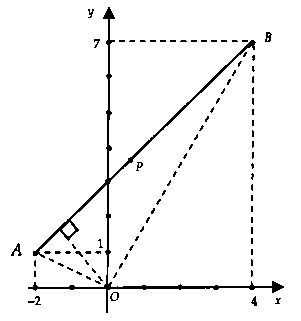
ight) = frac{{sqrt 2 }}{2}.$Chọn đáp án C.
Ví dụ 8: Cho số phức ${z_1}$ thỏa mãn $left| {{z_1} – 1 – 2i}
ight| = 2$ và số phức ${z_2}$ thỏa mãn $left| {{z_2} – 1}
ight| = left| {{z_2} + i}
ight|.$ Tính giá trị nhỏ nhất của $left| {{z_1} – {z_2}}
ight|.$A. $frac{{2sqrt 2 – 2}}{2}.$B. $frac{{3sqrt 2 – 4}}{2}.$C. $frac{{3sqrt 2 – 4}}{4}.$D. $frac{{3sqrt 2 – 2}}{4}.$
Lời giải:Gọi $P$, $Q$ lần lượt là điểm biểu diễn số phức ${{z_1}}$, ${{z_2}}$ trên mặt phẳng tọa độ.
$left| {{z_1} – 1 – 2i}
ight| = 2$ $ Rightarrow P in (C)$ có tâm $I(1;2)$, bán kính $R =2.$Gọi ${z_2} = {x_2} + {y_2}i$ $left( {{x_2};{y_2} in R}
ight).$$left| {{z_2} – 1}
ight| = left| {{z_2} + i}
ight|$ $ Leftrightarrow {x_2} + {y_2} = 0.$$ Rightarrow Q in d:x + y = 0.$Ta có: $left| {{z_1} – {z_2}}
ight| = PQ$ $ Rightarrow {left| {{z_1} – {z_2}}
ight|_{min }} = P{Q_{min }}$, $d(I;d) = frac{{3sqrt 2 }}{2}.$Từ hình vẽ ta có: $P{Q_{min }} = d(I;d) – R$ $ = frac{{3sqrt 2 }}{2} – 2$ $ = frac{{3sqrt 2 – 4}}{2}.$Chọn đáp án B.
Ví dụ 9: Cho số phức ${z_1}$ thỏa mãn $left| {{z_1} – 2 + i}
ight| = 1$ và số phức ${z_2}$ thỏa mãn $left| {{z_2} + 2i}
ight| = left| {{z_2} + 2}
ight|.$ Tính giá trị nhỏ nhất của $left| {{z_1} – {z_2}}
ight|.$A. $frac{{3sqrt 2 – 2}}{2}.$B. $frac{{3sqrt 2 – 2}}{4}.$C. $frac{{3sqrt 2 – 1}}{4}.$D. $frac{{3sqrt 2 – 1}}{2}.$
Lời giải: Gọi $M$, $N$ lần lượt là điểm biểu diễn số phức ${z_1}$, ${z_2}$ trên mặt phẳng tọa độ.
$left| {{z_1} – 2 + i}
ight| = 1$ $ Rightarrow M in (C)$ có tâm $I(2; – 1)$, bán kính $R=1.$Gọi ${z_2} = {x_2} + {y_2}i$ $left( {{x_2};{y_2} in R}
ight).$$left| {{z_2} + 2i}
ight| = left| {{z_2} + 2}
ight|$ $ Leftrightarrow {x_2} – {y_2} = 0.$$ Rightarrow N in d:x – y = 0.$Ta có: $left| {{z_1} – {z_2}}
ight| = MN$ $ Rightarrow {left| {{z_1} – {z_2}}
ight|_{min }} = M{N_{min }}$, $d(I;d) = frac{{3sqrt 2 }}{2}.$Từ hình vẽ ta có: $M{N_{min }} = d(I;d) – R$ $ = frac{{3sqrt 2 }}{2} – 1$ $ = frac{{3sqrt 2 – 2}}{2}.$Chọn đáp án A.
Ví dụ 10: Cho số phức ${z_1}$ thỏa mãn $left| {{z_1} – 2 – 3i}
ight| = 2$ và số phức ${z_2}$ thỏa mãn $left| {{z_2} + 1 + 2i}
ight| = left| {{z_2} + i}
ight|.$ Gọi $M$ là giá trị lớn nhất của $left| {{z_1}}
ight|$, $m$ là giá trị nhỏ nhất của $left| {{z_2}}
ight|.$ Giá trị $M – {m^2}$ bằng?A. $sqrt {13} + sqrt 2 – 2.$B. $sqrt {13} – 4.$C. $sqrt {13} .$D. $sqrt {13} – sqrt 2 – 2.$
Lời giải:Gọi $P$, $Q$ lần lượt là điểm biểu diễn số phức ${z_1}$, ${z_2}$ trên mặt phẳng.
$left| {{z_1} – 2 – 3i}
ight| = 2$ $ Rightarrow P in (C)$ có tâm $I(2;3)$, bán kính $R =2.$Gọi ${z_2} = {x_2} + {y_2}i$ $left( {{x_2};{y_2} in R}
ight).$$left| {{z_2} + 1 + 2i}
ight| = left| {{z_2} + i}
ight|$ $ Leftrightarrow {x_2} + {y_2} + 2 = 0.$$ Rightarrow Q in d:x + y + 2 = 0.$Từ hình vẽ ta có:$M = {left| {{z_1}}
ight|_{max }}$ $ = OB = OI + R$ $ = sqrt {13} + 2$, $m = {left| {{z_2}}
ight|_{min }}$ $ = d(O;d) = sqrt 2 .$$ Rightarrow M – {m^2} = sqrt {13} .$Chọn đáp án C.
Ví dụ 11: Cho số phức ${z_1}$ thỏa mãn $left| {{z_1} – 3 – 5i}
ight| = 2$ và số phức ${z_2}$ thỏa mãn $left| {{z_2} + 1 + 2i}
ight| = left| {{z_2} + i}
ight|.$ Tính giá trị nhỏ nhất của $left| {{z_1} – {z_2} – 1 – 2i}
ight|.$A. $frac{{5sqrt 2 – 4}}{2}.$B. $frac{{5sqrt 2 + 4}}{2}.$C. $frac{{7sqrt 2 – 4}}{2}.$D. $frac{{7sqrt 2 + 4}}{2}.$
Lời giải:Ta có: $left| {{z_1} – {z_2} – 1 – 2i}
ight|$ $ = left| {left( {{z_1} – 1 – 2i}
ight) – {z_2}}
ight|$ $ = left| {{z_3} – {z_2}}
ight|$ với ${z_3} = {z_1} – 1 – 2i.$
Gọi $M$, $N$ lần lượt là điểm biểu diễn số phức ${z_3}$, ${z_2}$ trên mặt phẳng tọa độ.$left| {{z_1} – 3 – 5i}
ight| = 2$ $ Leftrightarrow left| {underbrace {{z_1} – 1 – 2i}_{{z_3}} – 2 – 3i}
ight| = 2.$$ Rightarrow M in (C)$ có tâm $I(2;3)$, bán kính $R = 2.$Gọi ${z_2} = x + yi$ $(x;y in R)$, $left| {{z_2} + 1 + 2i}
ight| = left| {{z_2} + i}
ight|.$$ Leftrightarrow x + y + 2 = 0$ $ Rightarrow N in d:x + y + 2 = 0.$Ta có: $d(I;d) = frac{{7sqrt 2 }}{2}.$Từ hình vẽ ta có $M{N_{min }} = d(A;d)$ $ = d(I;d) – R$ $ = frac{{7sqrt 2 }}{2} – 2$ $ = frac{{7sqrt 2 – 4}}{2}.$Chọn đáp án C.
Ví dụ 12: Cho số phức $z$ thỏa mãn điều kiện $|z – 1 – i| + |z – 2 – 3i| = sqrt 5 .$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của môđun của $z.$ Giá trị ${M^2} + {m^2}$ bằng?A. $11.$B. $15.$C. $sqrt 2 + sqrt {13} .$D. $frac{{66}}{5}.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.
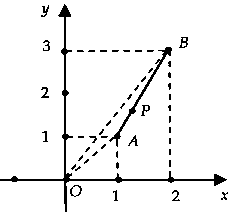
Ta có: $|z – 1 – i| + |z – 2 – 3i| = sqrt 5 .$$ Leftrightarrow sqrt {{{(x – 1)}^2} + {{(y – 1)}^2}} $ $ + sqrt {{{(x – 2)}^2} + {{(y – 3)}^2}} $ $ = sqrt 5 $ $(1).$Đặt $A(1;1)$, $B(2;3)$ thì từ $(1)$ ta có: $AP + BP = sqrt 5 $ $(2).$Mặt khác $AB = sqrt {{{(2 – 1)}^2} + {{(3 – 1)}^2}} = sqrt 5 $ $(3).$Từ $(2)$ và $(3)$ suy ra $P$ thuộc đoạn thẳng $AB.$Từ hình vẽ ta có:$M = |z{|_{max }} = OB = sqrt {13} $ và $m = |z{|_{min }} = OA = sqrt 2 $ $ Rightarrow {M^2} + {m^2} = 15.$Chọn đáp án B.
Ví dụ 13: Cho số phức $z$ thỏa mãn điều kiện $|z – 2i| + |z – 4 – 3i| = sqrt {17} .$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z|.$ Giá trị $M + m$ bằng?A. $sqrt 5 + sqrt 2 .$B. $frac{{8sqrt {17} }}{7} + 5.$C. $frac{{8sqrt {17} }}{7} + 2.$D. $7.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.
Ta có: $|z – 2i| + |z – 4 – 3i| = sqrt {17} .$$ Leftrightarrow sqrt {{x^2} + {{(y – 2)}^2}} $ $ + sqrt {{{(x – 4)}^2} + {{(y – 3)}^2}} $ $ = sqrt {17} $ $(1).$Đặt $A(0;2)$, $B(4;3)$ thì từ $(1)$ ta có: $AP + BP = sqrt {17} $ $(2).$Mặt khác $AB = sqrt {{{(4 – 0)}^2} + {{(3 – 2)}^2}} = sqrt {17} $ $(3).$Từ $(2)$ và $(3)$ suy ra $P$ thuộc đoạn thẳng $AB.$Từ hình vẽ ta có: $M = |z{|_{max }} = OB = 5$ và $m = |z{|_{min }} = OA = 2$ $ Rightarrow M + m = 7.$Chọn đáp án D.
Ví dụ 14: Xét các số phức $z$ thỏa mãn $|z + 2 – i| + |z – 4 – 7i| = 6sqrt 2 .$ Gọi $m$, $M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của $|z|.$ Giá trị $m + M$ bằng?A. $frac{{2sqrt {65} + 3sqrt 2 }}{2}.$B. $frac{{2sqrt {65} + sqrt 2 }}{2}.$C. $frac{{2sqrt {65} + sqrt 2 }}{4}.$D. $frac{{2sqrt {65} + 3sqrt 2 }}{2}.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.
Ta có: $|z + 2 – i| + |z – 4 – 7i| = 6sqrt 2 .$$ Leftrightarrow sqrt {{{(x + 2)}^2} + {{(y – 1)}^2}} $ $ + sqrt {{{(x – 4)}^2} + {{(y – 7)}^2}} = 6sqrt 2 .$Đặt $A( – 2;1)$, $B(4;7)$ thì từ $(1)$ ta có: $AP + BP = 6sqrt 2 $ $(2).$Mặt khác $AB = 6sqrt 2 $ $(3).$Từ $(2)$ và $(3)$ suy ra $P$ thuộc đoạn thẳng $AB.$Từ hình vẽ ta có: $M = |z{|_{max }} = OB = sqrt {65} .$$AB:frac{{x + 2}}{{4 + 2}} = frac{{y – 1}}{{7 – 1}}$ $ Leftrightarrow x – y + 3 = 0$, $m = |z{|_{min }}$ $ = d(O;AB) = frac{{3sqrt 2 }}{2}.$$ Rightarrow M + m = sqrt {65} + frac{{3sqrt 2 }}{2}$ $ = frac{{2sqrt {65} + 3sqrt 2 }}{2}.$Chọn đáp án A.
Xem thêm: Đơn Khiếu Nại Là Gì Và Những Thông Tin Pháp Lý Liên Quan, Hình Thức Và Nội Dung Khiếu Nại Được Quy
Ví dụ 15: Xét các số phức $z$ thỏa mãn $|z + 2 – i| + |z – 4 – 7i| = 6sqrt 2 .$ Gọi $m$, $M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của $|z – 1 + i|.$ Tính $P = m + M.$A. $P = sqrt {13} + sqrt {73} .$B. $P = frac{{5sqrt 2 + 2sqrt {73} }}{2}.$C. $P = 5sqrt 2 + sqrt {73} .$D. $P = frac{{5sqrt 2 + sqrt {73} }}{2}.$
Lời giải:Gọi $P(x;y)$ là điểm biểu diễn của số phức $z = x + yi$ $(x;y in R)$ trên mặt phẳng tọa độ.Số phức $z-1+i$ có điểm biểu diễn là $P”(x – 1;y + 1).$Ta có: $|z + 2 – i| + |z – 4 – 7i| = 6sqrt 2 .$$ Leftrightarrow sqrt {{{(x + 2)}^2} + {{(y – 1)}^2}} $ $ + sqrt {{{(x – 4)}^2} + {{(y – 7)}^2}} $ $ = 6sqrt 2 .$$ Leftrightarrow sqrt {{{((x – 1) + 3)}^2} + {{((y + 1) – 2)}^2}} $ $ + sqrt {{{((x – 1) – 3)}^2} + {{((y + 1) – 8)}^2}} $ $ = 6sqrt 2 $ $(1).$Đặt $A(-3;2)$, $B(3;8)$ thì từ $(1)$ ta có: $AP’ + BP’ = 6sqrt 2 $ $(2).$Mặt khác $AB = 6sqrt 2 $ $(3).$Từ $(2)$ và $(3)$ suy ra $P’$ thuộc đoạn thẳng $AB.$
Từ hình vẽ ta có: $M = |z{|_{max }} = OB = sqrt {73} .$$AB:$ $frac{{x + 3}}{{3 + 3}} = frac{{y – 2}}{{8 – 2}}$ $ Leftrightarrow x – y + 5 = 0.$$m = |z{|_{min }}$ $ = d(O;AB) = frac{{5sqrt 2 }}{2}.$$ Rightarrow M + m$ $ = sqrt {73} + frac{{5sqrt 2 }}{2}$ $ = frac{{2sqrt {73} + 5sqrt 2 }}{2}.$Chọn đáp án B.
III. LUYỆN TẬP1. ĐỀ BÀICâu 1: Cho số phức $z$ thỏa mãn điều kiện $|z + 1 – 3i| = 2.$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z|.$ Giá trị $M.m$ bằng?A. $14.$B. $1.$C. $8.$D. $6.$
Câu 2: Cho số phức $z$ thỏa mãn điều kiện $|z + 1 + i| = 3.$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z|.$ Giá trị $M – m$ bằng?A. $12.$B. $6.$C. $2sqrt 2 .$D. $3 + sqrt 2 .$
Câu 3: Cho số phức $z$ thỏa mãn điều kiện $|z – 2| = 2.$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $|z + i|.$ Giá trị $M – 2m$ bằng?A. $1.$B. $3sqrt 5 – 2.$C. $3sqrt 5 – 6.$D. $6 – sqrt 5 .$
Câu 4: Cho số phức $z$ thỏa mãn điều kiện $|z – 1| = |z + 1 – i|.$ Gọi $m$ là giá trị nhỏ nhất của $|z|.$ Giá trị $m$ bằng?A. $frac{1}{{20}}.$B. $frac{{sqrt 5 }}{{10}}.$C. $frac{1}{4}.$D. $frac{1}{2}.$
Câu 5: Cho số phức ${z_1}$ thỏa mãn điều kiện $left| {{z_1} + 1 – i}
ight| = left| {{z_1} + 2}
ight|$, số phức ${z_2}$ thỏa mãn điều kiện $left| {{z_2} – 1}
ight| = left| {{z_2} + i}
ight|.$ Gọi $m$ là giá trị nhỏ nhất của $left| {{z_2} – {z_1}}
ight|.$ Giá trị $m$ bằng?A. $2.$B. $frac{1}{2}.$C. $frac{{sqrt 2 }}{2}.$D. $frac{{sqrt 3 }}{3}.$
Câu 6: Cho số phức ${z_1}$ thỏa mãn $left| {{z_1} – 2 – 3i}
ight| = 1$ và số phức ${z_2}$ thỏa mãn $left| {{z_2} + i}
ight| = left| {{z_2} – 1}
ight|.$ Tính giá trị nhỏ nhất của $left| {{z_1} – {z_2}}
ight|.$A. $frac{{3sqrt 2 – 2}}{2}.$B. $frac{{3sqrt 2 – 2}}{4}.$C. $frac{{3sqrt 2 – 4}}{4}.$D. $frac{{3sqrt 2 – 4}}{2}.$
Câu 7: Cho số phức ${z_1}$ thỏa mãn $left| {(1 + i){z_1} + 1 – 5i}
ight| = 2sqrt 2 $ và số phức ${z_2}$ thỏa mãn $left| {{z_2} + 1 + 2i}
ight| = left| {{z_2} + i}
ight|.$ Gọi ${m_1}$ là giá trị nhỏ nhất của $left| {{z_1}}
ight|$, ${m_2}$ là giá trị nhỏ nhất của $left| {{z_2}}
ight|.$ Giá trị ${m_1} + {m_2}$ bằng?A. $sqrt {13} – 4.$B. $sqrt {13} – 2sqrt 2 .$C. $sqrt {13} – 2 + sqrt 2 .$D. $sqrt {13} + 2sqrt 2 .$
Câu 8: Cho số phức ${z_1}$ thỏa mãn $left| {{z_1} + 1 – 3i}
ight| = 2$ và số phức ${z_2}$ thỏa mãn $left| {{z_2} – 1 + i}
ight| = left| {{z_2} – i}
ight|.$ Gọi $M$, $m$ là giá trị lớn nhất của $left| {{z_1}}
ight|$ và giá trị nhỏ nhất của $left| {{z_2}}
ight|.$ Giá trị $M.m$ bằng?A. $frac{{2sqrt 5 + 5sqrt 2 }}{{10}}.$B. $frac{{5sqrt 2 – 2sqrt 5 }}{{10}}.$C. $frac{{10 + sqrt {10} }}{{10}}.$D. $frac{{5sqrt 2 – 2sqrt 5 }}{5}.$
Câu 9: Cho số phức $z$ thỏa mãn điều kiện $|z + 2 – i| + |z – 2 – 3i| = 2sqrt 5 .$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của môđun của $z$, tính $M+m.$A. $frac{{4sqrt 5 + 5sqrt {13} }}{5}.$B. $sqrt 5 + sqrt {13} .$C. $sqrt 2 + sqrt {13} .$D. $sqrt 2 + 2sqrt {13} .$
Câu 10: Cho số phức $z$ thỏa mãn điều kiện $|z + 2 – i| + |z – 2 – 3i| = 2sqrt 5 .$ Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của môđun của $z + 1 – 2i$, tính $M+m.$A. $frac{{2sqrt 5 + 5sqrt {10} }}{5}.$B. $frac{{sqrt 5 + 5sqrt {10} }}{5}.$C. $sqrt 2 + sqrt {10} .$D. $sqrt 2 + 2sqrt {10} .$