Lớp 1-2-3
Lớp 1
Lớp 2
Vở bài tập
Lớp 3
Vở bài tập
Đề thi
Lớp 4
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 5
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Lớp 6
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 7
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 8
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 9
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 10
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 11
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 12
Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề & Trắc nghiệm
IT
Ngữ pháp Tiếng Anh
Lập trình Java
Phát triển web
Lập trình C, C++, Python
Cơ sở dữ liệu

Loạt bài 700 Câu hỏi & Bài tập trắc nghiệm Toán lớp 12 phần Giải tích chọn lọc, cơ bản, nâng cao có lời giải chi tiết giúp bạn củng cố và ôn luyện kiến thức môn Toán 12 để chuẩn bị cho kì thi THPT Quốc gia.
Đang xem: Bài tập trắc nghiệm chương 2 giải tích 12
Mục lục Bài tập trắc nghiệm Giải tích 12
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Chương 2: Hàm số lũy thừa, hàm số mũ, hàm số logarit
Chương 3: Nguyên hàm, tích phân và ứng dụng
Chương 4: Số phức
Danh mục trắc nghiệm theo bài học
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Chương 2: Hàm số lũy thừa, hàm số mũ, hàm số logarit
Chương 3: Nguyên hàm, tích phân và ứng dụng
Chương 4: Số phức
Trắc nghiệm Toán 12 Bài 1 (có đáp án): Sự đồng biến nghịch biến của hàm số (phần 1)
Bài 1: Cho hàm số y = sin2x – 2x. Hàm số này
A.Luôn đồng biến trên R B. Chỉ đồng biến trên khoảng (0; +∞)
C. Chỉ nghịch biến trên (-∞; -1) D. Luôn nghịch biến trên R
Hiển thị đáp án
Tập xác định D = R
Ta có : y” = 2.cos2x – 2 = 2(cos2x – 1) ≤ 0; ∀ x
(vì -1 ≤ cos2x ≤ 1)
Vậy hàm số luôn nghịch biến trên R
Chọn đáp án D.
Bài 2: Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?
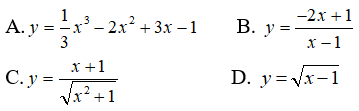
Hiển thị đáp án

Bài 3: Tìm m để hàm số
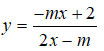
luôn nghịch biến trên khoảng xác định.
A.-2 2
C. -2 Hiển thị đáp án
Tập xác định
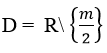
Hàm số nghịch biến trên từng khoảng
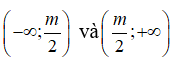
khi và chỉ khi
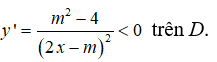
Suy ra m2 – 4
Bài 4: Cho hàm số y = -x3 + 3×2 + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
A. m Hiển thị đáp án
Ta có y” = -3×2 + 6x + 3m. Hàm số nghịch biến trên khoảng (0; +∞) nếu y” ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình -3×2 + 6x + 3m. Ta có Δ” = 9(1 + m)
TH1: Δ” ≤ 0 => m ≤ -1 khi đó, -3×2 + 6x + 3m 0 => m > -1; y” = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
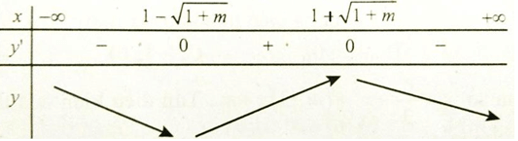
Hàm số nghịch biến trên (0; +∞) 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y” = -3×2 + 6x + 3m ≤ 0, ∀x > 0 3m ≤ 3×2 – 6x, ∀x > 0
Từ đó suy ra 3m ≤ min(3×2 – 6x) với x > 0
Mà 3×2 -6x = 3(x2 -2x + 1) – 3 = 3(x – 1)2 – 3 ≥ -3 ∀ x
Suy ra: min( 3×2 – 6x) = – 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1. Chọn đáp án C.
Bài 5: Cho đồ thị hàm số với x ∈ <- π/2 ; 3π/2> như hình vẽ.
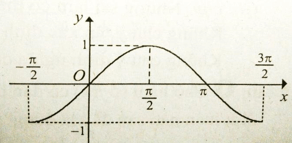
Tìm khoảng đồng biến của hàm số y = sinx với x ∈ <- π/2 ; 3π/2>

Hiển thị đáp án
Trên khoảng (-π/2; π/2) đồ thị hàm số đi lên từ trái sang phải.
Trên khoảng (π/2 ; 3π/2) đồ thị hàm số đi xuống từ trái sang phải.
Do đó hàm số đồng biến trên khoảng (-π/2; π/2)
Chọn đáp án A.
Xem thêm: You Too Nghĩa Là Gì – What Is The Meaning Of You Too
Trắc nghiệm Toán 12 Bài 2 (có đáp án): Cực trị của hàm số (phần 1)
Bài 1: Tìm tất cả các giá trị của tham số m để hàm số y = x3 – 2×2 +mx + 1 đạt cực đại tại x = 1.
A.m = -1 B. m = 1 C. m = 4/3 D. Không tồn tại.
Hiển thị đáp án
Ta có y” = 3×2 – 4x + m
Hàm số đạt cực trị tại x = 1 thì y”(1) = 0 ⇒ 3.12 – 4.1 + m = 0 ⇒ m = 1
Với m = 1 thì hàm số đã cho trở thành y = x3 – 2×2 + x + 1
Ta có y” = 3×2 – 4x + 1, y”” = 6x – 4 Vì y””(1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1.
Do vậy không có m thỏa mãn. Chọn đáp án D.
Chú ý. Sai lầm có thể gặp phải: khi giải y”(1) = 0 => m = 1 đã vội kết luận mà không kiểm tra lại, dẫn đến chọn đáp án B.
Bài 2: Cho hàm số y = x3 – 2×2 + 3. Điểm M(0; 3) là:
A.Cực đại của hàm số C. Điểm cực đại của đồ thị hàm số
B.Điểm cực đại của hàm số D. Điểm cực tiểu của đồ thị hàm số
Hiển thị đáp án
Ta có: y” = 3×2 -4x; y”” = 6x – 4;
y””(0) = -4
Bài 3: Tìm điểm cực đại của hàm số y = sin2x + √3cosx + 1 với x ∈ (0; π)
A. x = 0 B. x = π C. π/6 D. π/3
Hiển thị đáp án
Ta có:
Chọn đáp án C.
Bài 4: Có bao nhiêu mệnh đề đúng trong các phát biểu sau?
1.Hàm số không có đạo hàm tại x = 0.
2.Hàm số không liên tục tại x = 0.
3.Hàm số không có cực trị tại x = 0.
4.Hàm số đạt cực trị tại x = 0.
A.0 B. 1 C. 2 D. 3.
Xem thêm: Sách Học Tiếng Trung Cho Người Mới Bắt Đầu, Sách Tự Học Tiếng Trung Cho Người Mới Bắt Đầu
Hiển thị đáp án
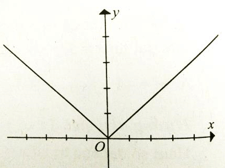
Đồ thị hàm số y = |x| có dạng hình vẽ.
Từ đồ thị trong hình ta có hàm số y = |x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó. Sử dụng định nghĩa cực trị ta có hàm số y = |x| đạt cực tiểu tại x = 0